Category Archives: amusement

Part II: Mass of the Death Star in Episode IV

Posted on by

This is the second in a two part post where I calculate the size and mass respectively of the Death Star in Episode IV (DS1).  Estimating the mass will inform discussion about the power source of the station and other energy considerations.

Part II: Mass of DS1

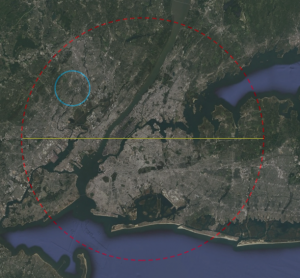
As argued in Part I, I assert that the diameter of DS1 is approximately 60 km based on a self-consistent scale analysis of the station plan schematics as shown during the briefing prior to the Battle of Yavin.

A “realistic” upper limit for the mass is set if the 60 km volume of DS1 was filled with the densest (real, stable) element currently known.  This is osmium with a mass density of 2.2E4 kilograms per cubic meter.  This places the mass at 2.5E18 kg with a surface gravity of 0.05g.  A filling fraction of 10% would then place a “realistic” estimate of the upper limit at 2.5E17 kg.  Other analyses have made similar assessments using futuristic materials with some volume filling-fraction, also putting the mass somewhere around 10^18 kg assuming a radius of 160 km.

In this mass analysis, using information from the available footage from the Battle of Yavin, I find a DS1 mass of roughly 2.8E23 kg, about million times the mass of a “realistic” approximation  Any supporting superstructure would be a small perturbation on this number.  This implies a surface gravity of an astounding 448g.  To account for this, my conclusion is that DS1 has a 40 m radius sphere of (contained) quark-gluon plasma or a 55 m radius quantity of neutronium at its core.  Such materials, if converted to useful energy with an efficiency of 0.1%, would be ample to 1) provide the 2.21E32 J/shot of energy required to destroy a planet as well as 2) serve as a power source for sub-light propulsion.

Details

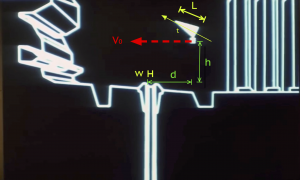
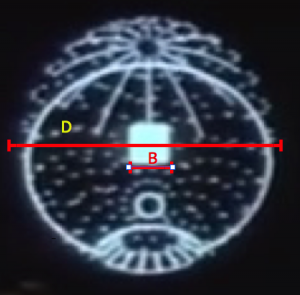
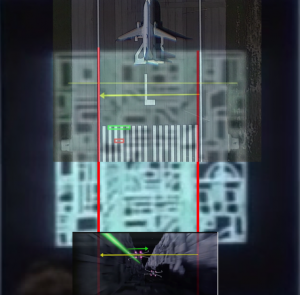
The approach here uses the information available in the schematics shown during the briefing.  The briefing displays a simulation of the battle along the trench to the exhaust port.  Again, as shown in Part I of this post, the simulation scale is self-consistent with other scales in both the schematic and the actual battle footage.  As shown in Figure 1, the proton torpedo is launched into projectile motion only under the influence of gravity.  It appears to be at rest with respect to the x-wing as it climbs at an angle of about 25 degrees.

Figure 1

Figure 2

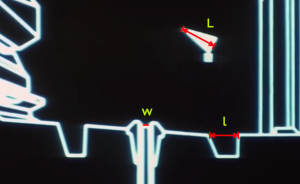
From the previous scale analysis in Part I, the distance from the port, d, and height, h, above the the port can be estimated.  They are approximately equal, h = d = 21 meters. The length of the x-wing is L = 12.5 m.  After deployment, the trajectory slightly rises and then falls into the exhaust port as shown in Figure 2.  A straightforward projectile motion calculation gives the formula for the necessary downward acceleration to follow the trajectory of an object under these conditions

a=\frac{2 V_{0}^2}{d}(\frac{h}{d}+\tan{\theta})\cos^2{\theta}\ \ \ \ (1)&s=3

Where t is the launch angle and Vo is the initial horizontal velocity of the projectile.  If we assume for simplicity that the angle \theta = 0 degrees and h = d, the formula simplifies to

a=\frac{2 V_{0}^2}{d}\ \ \ \ (2)&s=3.

From the surface gravity, the mass of can be obtained, assuming Newtonian gravity,

M=\frac{a R^2}{G}\ \ \ \ (3)&s=3.

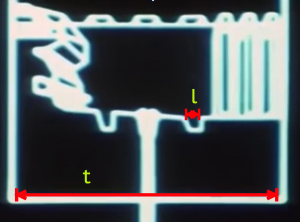
Here G = 1.67E-11 Nm/kg, the gravitational constant.  For a bombing run, let’s assume the initial speed of the projectile to be the speed of the x-wing coming down the trench.  To estimate the speed, v, of the x-wing, information from the on-board battle computers is used.  In Part I, the length of the trench leading to the exhaust port was estimated to be about x = 4.7 kilometers.  On the battle computers, the number display coincidentally starts counting down from the range of about 47000 (units not displayed).  However, from this connection I will assume that the battle computers are measuring the distance to the launch point in decimeters.  From three battle computer approach edits, shown in Clip 1 below, and using the real time length of the different edits, the speed of an x-wing along the trench is estimated to be about 214 meters/second (481 miles/hour).  This is close to the cruising speed of a typical airliner — exceptionally fast given the operating conditions, but not unphysical.  This gives a realistic 22 seconds for an x-wing to travel down the trench on a bombing run.

Using this speed and the other information, this places the surface gravity of DS1 at about 448 g (where g is the acceleration due to gravity on the surface of the earth).  DS1 would have to have a corresponding mass of 2.4E23 kg to be consistent with this.

However, it is clear that considerable liberty was taken in the above analysis and perhaps too much credibility was given to the battle simulation alone, which does not entirely match the dynamics show in the footage of the battle. Upon inspection of the footage, the proton torpedoes are clearly launched with thrust of their own at a speed greater than that of the x-wing.  A reasonable estimate might put v (torpedo) to be roughly twice the cruising speed of the x-wing.  Moreover, the torpedoes are obviously not launched a mere d = 21 meters from the port (although h = 21 is plausible), rather sufficiently far such that the port is just out of sight in the clip.  Finally, the torpedoes enter the port at an awkward angle and appear to be “sucked in.”  One might argue that there could be a heat seeking capability in the torpedo.  However, this seems unlikely.  If this were the case, then it greatly dilutes the narrative of the battle, which strongly indicates not only that the shot was very difficult but that it required the power of the Force to really be successful.  Clearly, “heat seeking missiles along with the power of the Force” is a less satisfying message.  Indeed, some have speculated that the shot could only have been made by Space Wizards.  These scenarios, and other realistic permutations, are in tension with the simulation shown in the briefing.  Based on different adjustments of the parameters v (torpedo), h, d, and th, one can tune the value of the surface gravity and mass to be just about anything.

However, if we attempt to be consistent with the battle footage, we might assume again that t=0 degrees while d = 210 m, and v (torpedo) = 2 v (x-wing) for propulsion.  The speed of the x-wing can remain the same as before at 214 m/s.  Even with this, the surface gravity will be 18g.  This still leads to a mass over 10000 times larger than the mass of a realistic superstructure.  In this case, a ball of neutronium 18 m in radius could still be contained in the center to account for this mass.

Nevertheless, my analysis is based on the following premise: the simulation indicates that the rebel analysts at least believed, based on the best information available, that a dead drop of a proton torpedo into the port, only under the influence of DS1’s gravity, was at least possible at d = h = 21 meters at the cruising speed of an x-wing flying along the trench under fire nap-of-the-earth.  Any dynamics that occurred in real time under battle conditions would ultimately need to be consistent with this.

The large intrinsic surface acceleration may seem problematic (consider tidal forces or other substantial technological complications).  However, as demonstrated repeatedly in the Star Wars universe, there already exists exquisite technology to manipulate gravity and create the appropriate artificial gravity conditions to accommodate human activities (e.g. within DS1, the x-wings, etc.) under a very wide range of activities (e.g. acceleration to hyperspace, rapid maneuvering of spacecraft, artificial gravity within spacecraft at arbitrary angles, etc.).

 

Implications for such a large mass.  

One hypothesis that would explain such a large mass would be to assume DS1 had, at its core, a substantial quantity of localized neutrinoium or quark-gluon plasma contained as an energy source.  Such a source with high energy density could be used for the purposes of powering a weapon capable of destroying a planet, as an energy source for propulsion, and other support activities.  For example, the destiny of neutronium is about 4E17 kilograms per cubic meter and a quark-gluon plasma is about 1E18 kilograms per cubic meter.  Specifically, a contained sphere of neutronium at the center of the death star of radius 55 meters would account for the calculated mass and surface gravity of DS1.

It has been estimated that approximately 2.4E32 joules of energy would be required to destroy an earth-sized planet.  If 6.7 cubic meters of neutronium (e.g. a sphere of radius 1.88 m) could be converted to useful energy with an efficiency of 0.1%, this would be sufficient to destroy a planet (assuming the supporting technology was in place).  This is using the formula

\Delta E=\epsilon\Delta m c^2\ \ \ \ (4)&s=3

where \Delta E is the useful energy extracted from a mass \Delta m with efficiency \epsilon.  The mass is converted to a volume using the density of the material.

By using the work-energy theorem, the energy required to accelerate DS1 to an arbitrary speed can be estimated.  Assuming the possibility for relativistic motion, it can be shown (left as an exerise for the reader) that the volume V of fuel of density \rho required to accelerate an object of mass M to a light-speed fraction \beta at efficiency \epsilon is given by

V=\frac{1}{\sqrt{1-\beta^2}}\left(\frac{M}{\epsilon\rho}\right)\ \ \ \ (5)&s=3.

This does not account for the loss of mass as the fuel is used, so represents an upper limit.  For example, to accelerate DS1 with M = 2.4E23 kg from rest to 0.1% the speed of light (0.001 c) would require about 296 cubic meters of neutronium (a sphere of radius 4.1 m).

From this, one concludes that the propulsion system may be the largest energy consideration rather than the primary weapon.  For example, consider DS1 enters our solar system from hyperspace (whose energetics are not considered here) and found itself near the orbit of mars.  It would take two days for it to travel to earth at 0.001 c.

 

Part I: Size of the Death Star in Episode IV

Posted on by

This is the first in a two part post where I calculate the size and mass respectively of the Death Star in Episode IV (DS1).  At the end of Part II I will discuss thoughts about the energy source of DS1.

Part I: Size of DS1

Conventional wisdom from multiple sources places the size of DS1 to about 100-160 km in diameter.  Based on an analysis of the station’s plans acquired by the Rebels, I estimate that the diameter of DS1 is 60 kilometers, not 100 km to 160 km.  To bolster the case, this scale is compared to other scales for self-consistency, such as the width of the trench leading to the exhaust port in the Battle of Yavin. Part II of the post will focus on the mass of DS1 using related methods.

To estimate the size of DS1, I will begin with the given length scale of the exhaust port w = 2 m.  This information was provided in the briefing prior to the Battle of Yavin where the battle strategy and DS1 schematics are presented.  This scale, when applied to Figure 1, is consistent with the accepted length of an x-wing L = 12.5 m.  I assume that the x-wing has an equal wingspan (there does not seem to be consistent values available).  I am also assuming that the “small, one-man fighter” referred to in the briefing is an x-wing, not a y-wing.  The x-wing is a smaller, newer model than the y-wing and it is natural to take that as the template.  The self-consistent length scales of w and L will establish the length calibration for the rest of the analysis.

Figure 1: A close up view of the exhaust port chamber during final phase of the bombing run.  The port width is given as w = 2 m.  The length of the x-wing is L = 12.5 m.  The forward hole, of length l, is then determined to be about 10 m.

From this, I extract the length of the smaller forward hole in Figure 1 to be approximately l = 10 m.

Figure 2: As the plans zoom out, a larger view of the exhaust port chamber of width t = 186 m.  The first hole is shown with width l = 10 m.  The scale of width l was determined based on information in Figure 1.  The width of t was determined based on the scale of l.

Using l as a calibration, this establishes the exhaust port chamber in Figure 2 to be approximately t = 186 m.

In Figure 3a and Figure 3b, circles of different radii were overlaid on the battle plans until a good match for the radius was established.  Care was taken to have the sphere’s osculate the given curvature and to center the radial line down the exhaust conduit.  From here, the size of the exhaust port chamber, of width t, was used as a calibration to approximate the diameter of DS1 as D = 60 km (red).  Several other circles are show in Figure 3 to demonstrate that this estimation is sensible: 160 km (purple), 100 km (black), and 30 km (blue).  It is clear that a diameter of 160 km is definitely not consistent with station’s schematics.  A diameter of 100 km is not wildly off, but is clearly systematically large across the range over the given arc length.  30 km is clearly too small.

While a diameter of 60 km may seem modest in comparison to the previously estimated 100 km to 160 km range, an appropriately scaled image of New York City is overlaid in Figure 4 to illustrate the magnitude of this systems in real-world terms; even a sphere of 60 km (red) is an obscenely large space station, considering this is only the diameter — more than adequate to remain consistentwith existing canon.  The size of the main ring of the LHC (8.6 km) is overlaid in light blue, also for scale.

Figure 3a (to the right of the exhaust port chamber): As the plans zoom out further, the exhaust port chamber of width t = 186 m is shown with the curvature of DS1 (the square blob is the proton torpedo that has entered the port).  The scale of t was determined based on information in Figure 2.  Several circles with calibrated diameters based on the scales set in Figures 1 and 2 are shown.  The 60 km diameter circle in red is arguably the best match to the curvature.  Care was taken to match the point of contact of the circles to a common central location along the radial port.

Figure 3b (to the left of the exhaust port chamber): The same idea as Figure 3a.  The 60 km diameter is still arguably the best match, although is a little shy on this side. The 100 km diameter, the next best candidate, is shooting higher than the 60 km is shooting low. Since an exact mathematical fit wasn’t performed, the expected radius is probably a bit higher than 60 km, but significantly lower than 100 km.

 

 

Figure 4: A 60 km diameter circle in red (with yellow diameter indicator) shown overlaid on a Google Earth image of the greater New York City region.  The blue ring is an overlay of the scale of the Large Hadron Collider at CERN (about 8.5 km in diameter) — note the blue ring is not a scaled representation of the main weapon!  The main message here is that a 60 km station, although smaller than the accepted 100-150 km, is still freakin’ HUGE.  At this scale, there is only a rather modest indication of the massive urban infrastructure associated with New York City.

As another check on self-consistency, the diameter D is then used to calibrate the successive zooms on the station schematics, as shown in Figures 5 and 6.  The length B = 10 km is the width of the zoom patch from Figure 5, X = 4.7 km is the length of the trench run, and b = 134 m is the width of one trench sector. From Figure 6, the width of the trench is estimated to be b’ = 60 m, able to accommodate roughly five x-wing fighters lined wingtip-to-wingtip.  This indicates that the zoom factor is about 1000x in the briefing.

Figure 7 is a busy plot.  It overlays several accurately scaled images over the 60 m trench, shown with two parallel red lines, to reinforce plausibility.  Starting from the top: an airport runway with a 737 ready for takeoff (wingspan 34 m); a 100 m-wide yellow calibration line; a 60 m-wide yellow calibration line; the widths of an x-wing (green, Wx = 12.5 m, where I’ve assumed the wingspan is about the same as the length — there does not seem to be a consensus online; I’ve seen the value quoted to be 10.9 m, but it isn’t well-sourced) and tie fighter (red, 6.34 m); and a scaled image from footage of two x-wings flying in formation, with a yellow 60 m calibration line as well as a calibrated green arrow placed over the nearer one to indicate 12.5 m.  As predicted, about five x-wings could fit across based on the still image.  Also from this, the depth of the trench is estimated to also be 60 m.  The scales are all quite reasonable and consistent. It is worth noting that if the station were 100 km, the next possible sensible fit to the arc length in Figure 3, the width of the trench would be about 100 m, twice the current scale.  This would not be consistent with either the visuals from the battle footage or the airport runway scales.

In short, while there is certainly worthy critique of this work, I argue that, after a reasonably careful analysis of the stolen plans for DS1, all scales paint a self-consistent picture that the diameter of DS1 is very close to 60 km.

Figure 5: A zoom-out of DS1 in the briefing based on the stolen battle plans.  D = 60 km is the diameter and B = 10 km is the width of the patch in the region of interest near the exhaust port.

Figure 6: A zoom in in the region of interest patch near the exhaust port channel (see Figure 5) with B = 10 km.  the channel itself is about X = 4.7 km long.  The width of the channel is about b = 134 m.  Inset is a further zoom of the insertion point along the channel.  Width of the channel itself is about b’ = 60 m.

Figure 7: A zoom of the insertion point along the channel for the bombing run.  Several elements are overplayed for a sense of scale and for consistency comparisons.  The red parallel lines represent the left and right edges of the channel.  From the top of the figure is a 737 with a wing span of 34 m.  The 737 is on a runway (at SFO).  Down from the 737 is a  yellow line that represents 100 m.  This would be the width of the channel if D = 100 km, which is clearly much too large based on the battle plans.  The next horizontal yellow arrow is the 60 m width based on the scales assumed with D = 60 m.  Next down, embedded in the vertical lines of the runway: a green block representing the width of an x-wing and a red block representing the width of a tie fighter.  Finally, at the bottom is a shot from the battle footage.  It has been scaled so the edges of the walls match the width of the channel (shown as a horizontal yellow arrow).  The width of the near x-wing is shown with a green horizontal arrow, which matches the expected scale of an x-wing.

 

The Best Nest

Posted on by
A0742B3C-042C-4203-B8E2-CD22B81D2971

The Best Nest by P.D. Eastman

 

The classic children’s book The Best Nest by children’s author P.D. Eastman, published in 1968, is one of the books that really sticks with me from my childhood.

I recall my mom reading it to me when I was about four or five. I’ve read it to my kids for years and my four-year-olds particularly adore it. It is the simple story of how a mama and papa bird go through a series of misadventures in an effort to find a new home, only to discover that their original home was really the best one after all. We find out at the end that the mama bird was ready to lay an egg and the whole effort was driven by her motherly instinct to find a safe space for her baby. It is sappy, and reinforces certain gender stereotypes, but is ultimately good-natured. While simple, it does follow the classic hero’s journey. After hardship and adventure, you find your way back to where you started as changed person (or bird, in this case), now wiser to the ways of the world (like not to nest in bell towers). When we got it for my kids years ago, I had instant flashbacks with the artwork, recalling fixations I’d had with certain details that, as an adult, I would never have noticed: the way the straw stuck out in their mouths, the particular hat the mama bird wore, the particular angle and character of the rain that came down on the papa bird at the end. All of it jumped out again.

 

879ABDAA-6F12-450D-A1CF-AB83334CA602

The church in the town featured in The Best Nest

One of the big turning points in the story is when the birds find this wonderful space for their nest. It is huge. It has all sorts of great views of the area. The mother bird thinks it is the best place. However, we, the reader, know that something will go terribly wrong: the space is really a bell tower for a church. The papa bird goes out to find new materials for their nest while the mama sets up shop. Well, sure enough, a funky beatnik proto-hippy guy named Mr. Parker, comes to the church and rings the hell out of that bell like he has no other outlet for his life’s frustrations.  The guy clearly loves his job. The papa bird comes back to find the place littered with bird feathers and no mama bird. He fears the worst and goes on a quest to find her.

Oberlander R.D. #1 Waldoboro, Ma...

Oberlander, R.D. #1, Waldoboro, Ma…

Before they find the bell tower, they look in other places for a new nest. One of the potential nests is a mailbox. Now, as I mentioned, as a kid I had particular fixations in details I would never had seen as an adult; conversely, in reading it to my children, I also found details I would never have found as a kid.  For example, one of the reasons they decided not to pick the mailbox is that, while they were checking it out, a mailman comes by and puts some mail into the mailbox.  Definitely not an ideal space for a pair of birds.

However, the piece of mail has an address on it (upside down in the text of the book):

…Oberlander
R.D. #1
Waldoboro, Ma…
Circa 2016, there is indeed an [Old] Road 1 in Waldoboro, Maine.  There is also an Oberlander family name that appears in that town’s older records.  That’s sort of neat.  Naturally, using Google Streeview, I wandered around to see if I could find the church where the bell tower was.  While not definitive, I have two candidates.  Sure, these churches are pretty generic shapes for the area.  Nevertheless, with a specific town to focus on, you can be pretty sure it must be one of two churches, or a composite, that P.D. used as a template.  He could have also just made something up from memory or imagination.
The first one, Broad Bay Congregational Church, has the correct weathervane, the correct three-window structure, a circular region in the middle, and an obvious bell tower.  It also has a front that is roughly consistent with the drawing, although obviously updated (e.g. it has two windows on each side of the door).
Waldoboro Broad Bay Congregational Church, 941 Main St, Waldoboro, Maine)

Waldoboro Broad Bay Congregational Church 941 Main St, Waldoboro, Maine

The second one, Waldoboro United Methodist Church, also has the three window configuration in the side, has similar slats near the bell tower as the drawing in the story (the slats were one of the weirdly specific things I fixated on as a child), and a pointy tower that resembles the one in the drawing.  But it does not have the right window configuration, the weathervane, nor the circular slats.
Waldoboro United Methodist Church (side view), 85 Friendship Street (Route 220), Waldoboro, Maine)

Waldoboro United Methodist Church (side view) 85 Friendship Street (Route 220), Waldoboro, Maine

Waldoboro United Methodist Church (front view), 85 Friendship Street (Route 220), Waldoboro, Maine.

Waldoboro United Methodist Church (front view), 85 Friendship Street (Route 220), Waldoboro, Maine.

My hunch is that the first one, Broad Bay Congregational Church, is the one in the story.  I suspect that during the time since P.D. Eastman wrote the story (circa 1968),  it has had a few upgrades.
But, as I said earlier, these are very common generic “Protestant-style” East Coast churches.  The story might have nothing to do with these specific churches.
Anyway, I had fun with this little distraction.  If anyone knows more about this Easter egg planted by P.D. Eastman, about any connection he may have had to the Waldoboro region, or the reason he might have picked “Oberlander” for the recipient of the letter on R.D #1, I’d love to hear about it.

Reading Audiobooks

Posted on by

If you listened to an audiobook is it responsible to say in conversation that you “read the book” without qualifying that it was an audiobook? Does listening to an audiobook constitute “reading a book”? The answer is “yes,” although this will require some explanation. The question sounds strange because I just said that you listened to it, and didn’t read it, didn’t I? And “reading” isn’t “listening” so how can listening to an audiobook allow one to claim one has “read the book”? I think some of this discussion is motivated by my own enjoyment of audiobooks in the face of those who can only be called “reading snobs” who dogmatically believe that books can only be “properly” processed one way: via the written text and with one’s eyes. There also may be a perception that listening to an audiobook is somehow easier or intellectually lighter than reading the text of a book. To this I say: try listening to an audiobook sometime. In my experience, audiobooks can be very intellectually satisfying and may even be a heavier cognitive load than reading text because your eyes are free to roam and process independent information. This forces no small measure of mental discipline to remain focused and engaged but still function (e.g. if you are walking or driving).

I just listened to David Brin’s excellent Uplift War on audiobook, and unapologetically declare to the world that I “read the book.” For full disclosure, I’ve also read Martian Chronicles by Ray Bradbury, all three Hunger Games novels by Suzanne Collins, Sara Gruen’s Water for Elephants, Neverwhere by Neil Gaiman, Packing for Mars by Mary Roach, and Letters to a Young Contrarian by Christopher Hitchens, amongst others. All on audiobook. From a social point of view, if you and I got together to discuss these works, my experience of them would be such that you would not be able to determine by our conversation if I listened to it or physically read the words on a page. In this sense, I can responsibly claim to have “read the book” even if my eyes never looked at the words. That is, using Brin’s work as an example, unless you asked me to spell the names “Uthacalthing”, “Tymbrimi”, or “Athaclena” (which I did not know how to spell until I looked them up just now) — but then I’d ask you to pronounce them and we’d be even.

There are two elements to consider: 1) reading as a physical method of information transfer and 2) reading as an intellectual exercise involving mental content absorption. Both senses of the term “read” are used regularly and interchangeably and we will need to remind ourselves what is really important. Certainly a quick scan of the dictionary (and one’s own experience) demonstrates the word “read” in the English language is used in many different ways. One of those ways is the specific biomechanical method of scanning physical symbols with one’s eyes. However, that same exact sense of the term also describes the methods of a person using their fingers to process braille symbols. Feeling something is biomechanically and mentally nothing like seeing it, but we are still comfortable using “read” in that context, allowing “read” to span the senses because it accomplishes the same intellectual function as reading symbols with one’s eyes. This is important. Other grammatically correct uses of the word “read” also include a broader defintions involving generalized mental information processing and experiences. Phrases like “I read you loud and clear” (e.g. for a radio transmission, when listening), “reading a situation” (assessing the subtleties of a situation, including your own intellect), performing “a cold reading” (another situational assessment tool used by magicians and “psychics” involving both mental acuity and all the senses), “I’m taking a sensor reading” (to describe a technology-based data acquisition process), and so on. For the primary defintions of “read” Merriam-Webster is actually rather non-committal about the method and focuses on generic sensory information processing, definitely emphasizing the written text and braille, but not insisting upon it, allowing for many other modes.

In this spirit, let’s examine what people mean in conversation about a work of fiction when they say “I read the book” or ask “did you read the book?” Let’s assume we are dealing with educated adults and not people just learning to read text. I assert that what people universally mean by the question “did you read the book?” is “did you intellectually and emotionally absorb and process the content of the work that was created by the author?” If I listened to an unabridged audiobook in an active and engaged way, I think the answer is unambiguously “yes, I read the book.” Sure, from a methodological point of view, I did not literally (literally) read the physical text on the page with my eyes. However, this is not usually the important part of the novel, nor is it generally the important part of “reading novels.” The mechanics of looking at words is not typically the essential experience of reading books. The important part is mentally absorbing the content of the work, which is actually the core definition of the word “read” to begin with. Why would anyone care about your particular mode of information transfer? What they (hopefully!) care about is the experience you had intellectually and emotionally absorbing the content and your ability to discuss that experience in a way that transcends the transfer mode.

Do all books lend themselves to this audio mode of reading? No. Obviously not. Exceptions include works that rely directly on the shapes of words or encoding extra information in the precise layout of the text, font, or presentation. If the work involves lots of pictures, illustrations, data, or equations, audiobooks are not going to work very well. But the bulk of modern fiction lends itself wonderfully to audiobooks as does much non-fiction. Like so many other things in life, one needs to account for individual cases. Also, this equivocation is not appropriate for people (e.g. children) learning to read symbols on the page. An audio experience is not an adequate substitute for that kind of information processing during those fragile formative years. This argument is directed at people who have mastered both reading and listening and are educated adults.

To be clear, I’m not suggesting we follow the reductio ad absurdum path and call all forms of information processing “reading” in every context for all conversations. That is a straw man of my argument. I’m merely suggesting that actively listening to an unabridged audiobook can, for social and intellectual purposes, be considered “reading a book” based on the sense of the word “read” one uses in conversations of that kind. There is nothing more I would gain from a content or entertainment perspective by re-reading the book using physical text in order to “elevate” myself to “having read the [text of] the book.” Nor am I suggesting that we substitute listening to audiobooks in place of reading text in schools, although I do think both forms could be used in tandem or parallel. As mentioned above, reading symbols is obviously a critical core skill that must be developed actively and early. But, once mastered, I assert that the two forms of information processing, listening and reading, blur into each other and naturally compliment each other. And I’m certainly not dismissing the process of reading physical text as an intellectual and worthy exercise. I still read many books this way. Also, I’m not claiming that there is absolutely no difference cognitively between how the brain processes words and symbols and how it processes sounds. But I do think that in the case of listening to a word-for-word reading of unabridged audiobooks, and for the educated person who has mastered both reading and listening, the audio experience and the reading experience merge for all practical purposes into a common intellectual experience with only minor variations that do not favor systematically one mode over another except by the taste of the user.

A couple tangential examples, that inform the discussion. A formally trained and competent musician can look at a piece of written music and, for all practical purposes, “listen” to it by reading it with their eyes. The audio performance itself, of course, also has aesthetic value for that musician. But it would probably be appropriate for someone in that position to say, in either context, that they “listened” or “heard” the piece even if it merely involved reading the sheet music. Indeed, musicians who can read written music like that do refer to reading sheet music as having “heard” or having “listened” to the piece. In contrast, many bands we worship refer to “writing” music for their albums. However, rarely are any notes or music written down in any formal sense. Many rock/pop bands “write” music by playing it and piecing together sections into things than sound nice after editing (if they are lucky). Later, some music grad student, desperate to eat and pay rent, will be hired by a company to transcribe the sounds on the album into written notes, so other people without ear training can also play the songs; but that isn’t the way the band itself usually “writes” music — unless you are Yes or Dream Theater. If the Rolling Stones speak of “writing” music for a new album, they almost certainly mean a wanton, drug-infused geriatric orgy in the Caribbean that might have involved Keith Richards bringing his guitar. But the term “writing music” is still used. We can also reverse the situation and look at words on a page that were meant to be spoken out loud, such as plays. Take Shakespeare. Certainly the stage play is considered a respectable form of literary art and Shakespeare is arguably the greatest writer of the English language. But the plays he wrote were meant, designed, crafted to be read aloud and listened to. Yet we read them. Can you still read Shakespeare and claim to have experienced the work in an intellectually satisfying way and be conversational about it? Obviously. Does the stage work bring the work to life in a different way? Clearly.

Also, reading words on a page is not itself a magic recipe for intellectual absorption. Reading text can be pathologically passive if one is not actively engaged, and does not imply extra profound and deep understanding. Let me give an example from my own experience in the classroom. I tell students to “read chapter 10” from the text. And, indeed some do look at it with their eyes and the words are streamed through their thinking in some fashion. But in many cases no cognitive engagement has occurred. By speaking to them, I can tell that they did not, in fact, “read” the text as I meant the term “read.” In this context, “read” did not necessarily literally mean merely looking at the words, although it might conveniently involve that biomechanical process. I really just wanted them to come to class having processed and understood the material provided in the book by whatever means necessary. If that involves listening to the audiobook, it just doesn’t matter to me (although, good luck learning quantum mechanics from an audiobook).

Does watching a movie adaptation of a book count as “reading the book?” Not in my opinion. Putting audiobooks in the same category as movie interpretation of books is missing the point. I claim the unabridged audiobook is not, fundamentally, a different medium than the original work — not any different than the braille modes of reading that are considered “legitimate” reading. When we read books using the written word we are, in fact, “speaking” the words to ourselves in our head anyway exactly in the way the book is being read in an audiobook. A movie, even one adapted to be nearly identical to the book, is usually abridged and has been altered from the original work in fundamentally different ways. Moreover, one is not required to visualize the plot and characters in the same way as one does in reading text or listening to a reading of text.

I am not judging all these different modes or ranking them. They each serve their purpose and can give pleasure and intellectual stimulation in their own way. But I argue that, under many common situations, listening to audiobooks accomplishes the same social and intellectual function as reading text and can thus be responsibly declared a form of “reading the book.”

The Universe: A Computer Simulation?

Posted on by

An unpublished paper on the arXiv is claiming to have formulated a suite of experiments, as informed by a particular kind of computer approximation (called “lattice QCD” or L-QCD), to determine if the universe we perceive is really just an elaborate computer simulation. It is creating a buzz (e.g. covered by the Skeptics Guide to the Universe, Technology Review, io9, and probably elsewhere).

I have some problems with the paper’s line of argument. But let me make it clear that I have no fundamental problem with the speculation itself. I think it is a fun and interesting to ponder the possibility of living in a simulation and to try and formulate experiments to demonstrate it. It is certainly an amusing intellectual exercise and, at least in my own experience, this was an occasional topic of my undergraduate years. More recently than my undergraduate years, Yale philosopher Nick Bostrom put forth this famous arguments in more quasiformal terms, but the idea had been hovering there (probably with a Pink Floyd soundtrack) for a long time.

The paper is not “crackpot”, but is highly speculative. It uses a legitimate argumentation technique, if used properly (and the authors basically do), called reductio ad absurdum: reduction to the absurd. Their argument goes like this:

  1. Computer simulations of spacetime dynamics, as known to humans, always involve space and time lattices as a stage to perform dynamical approximations (e.g. finite difference methods etc.);
  2. Lattice QCD (L-QCD) is a profound example of how (mere) humans have successfully simulated, on a lattice, arguably the most complex and pure sector of the Standard Model: SU(3) color, a.k.a. quantum chromodynamics, the gauge theory that governs the strong nuclear force as experienced by quarks and gluons;
  3. L-QCD is not perfect, and is still quite crude in its absolute modern capabilities (I think most people reading these articles, given the hype imparted to L-QCD, would be shocked at how underwhelming L-QCD output actually is, given the extreme amount of computing effort and physics that goes into it). But it is, under the hood, the most physically complete of all computer simulations and should be taken as a proof-of-principle for the hypothetical possibility of bigger and better simulations — if we can do it, even at our humble scale, certainly an übersimulation should be possible with sufficient computing resources;
  4. Extrapolating (this is the reductio ad absurdum part), L-QCD for us today implies L-Reality for some other beyond-our-imagination hypercreatures: for we are not to be taken as a special case for what is possible and we got quite a late start into the game as far as this sentience thing goes.
  5. Nevertheless, nuanced flaws in the simulation that arise because of the intrinsic latticeworks required by the approximations might be experimentally detectable.

Cute.

Firstly, there is an amusing recursive metacognative aspect to this discussion that has its own strangeness; it essentially causes the discussion to implode. It is a goddamn hall of mirrors from a hypothesis testing point of view. This was, I believe, the point Steve Novella was getting at in the SGU discussion. So, let’s set aside the question of whether a simulation could

  1. accurately reconstruct a simulation of itself and then
  2. proceed to simulate and predict its own real errors and then
  3. simulate the actual detection and accurate measurement of the unsimulated real errors.

Follow that? For the byproduct of a simulation to detect that it is part of an ongoing simulation via the artifacts of the main simulation, I think you have to have something like that. I’m not saying it’s not possible, but it is pretty unintuitive and recursive.

My main problem with the argument is this: a discrete or lattice-like character to spacetime, with all of its strange implications, is neither a necessary nor sufficient condition to conclude we live in a simulation. What it would tell us, if it were to be identified experimentally, is that: spacetime has a discrete or lattice-like character. Given the remarkably creative and far-seeing imaginative spirit of the project, it seems strangely naive to use such an immature, vague “simulation = discrete” connection to form a serious hypothesis. There very well may be some way to demonstrate we live in a simulation (or, phrased more responsibly, falsify the hypothesis that we don’t live in a simulation), but identifying a lattice-like spacetime structure is not the way. What would be the difference between a simulation and the “real” thing. Basically, a simulation would make error or have inexplicable quirks that “reality” would not contain. The “lattice approximation errors” approach is pressing along these lines, but is disappointingly shallow.

The evidence for living in a simulation would have to be much more profound and unsubtle to be convincing than mere latticworks. Something like, somewhat in a tongue-and-cheek tone:

  1. Identifying the equivalent of commented out lines of code or documentation. This might be a steganographic exercise where one looks for messages buried in the noise floor of fundamental constants, or perhaps the laws of physics itself. For example, finding patterns in π sounds like a good lead, a la Contact, but literally everything is in π an infinite number of times, so one needs another strategy like perhaps π lacking certain statistical patterns. If the string 1111 didn’t appear in π at any point we could calculate, this would be stranger than finding “to be or not to be” from Hamlet in ASCII binary;
  2. Finding software bugs (not just approximation errors); this might appear as inconsistencies in the laws of physics at different periods of time;
  3. Finding dead pixels or places where the hardware just stopped working locally; this might look like a place where the laws of physics spontaneously changed or failed (e.g. not a black hole where there is a known mechanism for the breakdown, but something like “psychics are real”, “prayer works as advertised”, etc.);

I’m just making stuff up, and don’t really believe these efforts would bear fruit, but those kinds of thing, if demonstrated in a convincing way, would be an indication to me that something just wasn’t right. That said, the laws of physics are remarkably robust: there are no known violations of them (or nothing that hasn’t been able to be incorporated into them) despite vigorous testing and active efforts to find flaws.

I would also like to set a concept straight that I heard come up in the SGU discussion: the quantum theoretical notion of the Planck length does not imply any intrinsic clumpiness or discreteness to spacetime, although it is sometimes framed this way in casual physics discussions. The Planck length is the spatial scale where quantum mechanics encounters general relativity in an unavoidable way. In some sense, current formulations of quantum theory and general relativity “predict” the breakdown of spacetime itself at this scale. But, in the usual interpretation, this is just telling us that both theories as they are currently formulated cannot be correct at that scale, which we already hypothesized decades ago — indeed this is the point of the entire project of M-theory/Loop quantum gravity and its derivatives.

Moreover, even working within known quantum theory and general relativity, to consider the Planck length a “clump” or “smallest unit” of spacetime is not the correct visualization. The Planck length sets a scale of uncertainty. The word “scale” in physics does not imply a hard, discrete boundary, but rather a very, very soft one. It is the opposite of a clump of spacetime. The Planck length is then interpreted as the geometric scale at which spacetime is infinitely fuzzy and statistically uncertain. It does not imply a hard little impenetrable region embedded in some abstract spacetime latticeworks. This breakdown of spacetime occurs at each continuous point in space. That is, one could zoom into any arbitrarily chosen point and observe the uncertainty emerge at the same scale. Again, no latticeworks or lumpiness is implied.

Forwards Backwards Songs

Posted on by

As a musical exercise, I’ve been experimenting with taking standard, famous songs and arranging a backwards version as a forward song (“backwards forwards” for short). I don’t use the original recording in any way, only part of the musical arrangement. The result is usually something that (naturally) has weird overtones of the original song, but also is a unique song in its own right.

My first effort was at tune called My Sweet Satan, an instrumental backwards forwards version of Stairway to Heaven by Led Zeppelin. The title is a play off of the famous backmasking fiasco that followed the song through its heyday and beyond. The haunting refrain of “my sweet Satan” can apparently be heard in verse five (somewhere around “There’s still time to change the road you’re on”). However, if you listen, it is clearly a combination of audio pareidolia and straightforward phonetic reversal rather than active backmasking. One can, of course, carefully craft forwards lyrics that do have phonetic reversals that sound like actual messages when played backwards. But Robert Plant’s lyric clearly isn’t that. I’ve tried doing such constructions myself and, with a specific backwards message in mind, you certainly don’t get anything nearly as coherent as the lyrics to Stairway (and that’s saying something).

Another effort is called But You Can Never Leave. Can you guess which backwards forward song it might be? A hint is that it is a song known (apocryphally) for having a backmasked message. The biggest clue is in the title.

If you like what you hear, take a listen to some of work by Agapanthus and consider purchasing it (or parts you like). You can also find many of my tunes on YouTube or Spotify under Agapanthus for free.

Mathematica One-Liner Competition 2012

Posted on by

Decided to enter Wolfram’s Mathematica One-Liner Competition 2012:  “What can you do with one line of code?”  That is, in under 140 characters (making it tweetable).  Why, a Particle Zoo Calliope, of course! My entry (only slightly modified from that submitted):

SectorChart[
Button[{1, p[#, s]},
EmitSound@Sound@SoundNote@{2 p[#, s], Floor@p[#, "Mass"]^.3}]
/.s -> "Spin" & /@ ParticleData[] /. p -> ParticleData]

W00t! Received an Honorable Mention! (the competition was fierce, lots of good one-liners). Give it a try below. You will need the free Mathematica CDF plugin installed. A figure will be generated. It is a musical instrument. Click on different locations on the figure to play different intervals. The first click is sometimes a bit awkward/slow, but after that it should play in real time.


Description:
A sector plot is generated based on the spin of all the known elementary particles (quarks, leptons, and gauge bosons) and the hadronic bound states (bayrons and mesons). The length of the tine on the sector plot is proportional to the particle’s intrinsic spin. There are around 1000 particles in the database. When you click on one of the sectors, representing a particle, two tones are played based on the spin and the mass of that particle. The mapping from values to notes is arbitrary, but selected to be “listenable.” I take two times the particle’s spin as one note and the integer part of the particle’s mass to the 0.3 as the second (this was selected by trial and error to give a reasonable range of tones for the full particle mass spectrum). A value of “0” is considered middle C and each integer above and below is a half-step.